 Python is a great language for exploration. Back in the old days I did a lot of programming using C++ and Microsoft's Component Object Model (COM). C++ COM is a fairly complex technology so I found it preferable to prototype object-oriented designs using Java. The Java language's interface mechanism was a good analog for COM's interface-based programming paradigm. Java was a sexy thing compared to COM and Java was the lingua-franca of object oriented design during this period.
Python is a great language for exploration. Back in the old days I did a lot of programming using C++ and Microsoft's Component Object Model (COM). C++ COM is a fairly complex technology so I found it preferable to prototype object-oriented designs using Java. The Java language's interface mechanism was a good analog for COM's interface-based programming paradigm. Java was a sexy thing compared to COM and Java was the lingua-franca of object oriented design during this period.Then I discovered Python and found that it featured a familar approach to object orientation and it looked like it would support rapid prototyping and concept exploration.
Python proved to be a excellent language, but it did not serve well as a prototypical language for C++ applications. In the C++ language, data types are everything. Most of the advanced features of the language, such as templates and classes, provide ways to manage functionality across data types. The C++ compiler is the ultimate master and the programmer is subjected to its rule of type.
Python cannot be used to prototype solutions to C++ problems because the problems do not appear in Python.
Most circa 2000 C++ programmer were ill-equipped to absorb Python. To absorb Python meant to be influenced and changed by Python - to refute idioms previously held sacrosanct.
To close the loop, a next logical step would be to gain perspective by relating Python to functional programming languages and not just to Java and C++.
My Python Data Structures Project
I go through a cycle every now and again that involves Python and data structures. A good data structure to code is the Priority Queue. The binary heap-based Priority Queue features a tree data structure, implemented using an array and clever array index manipulations. A binary min heap is shown below. Essential a binary heap must always be correctly ordered, children must always be greater than its parents (in the case of the binary min heap).

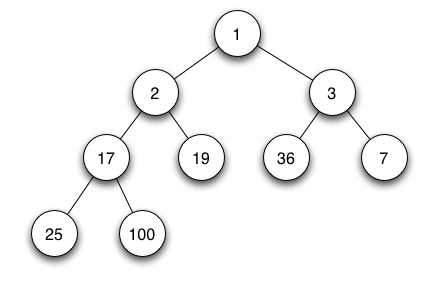
The binary heap is stored in a simple array. Algorithms maintain the relations between array elements as shown below. One exception is that it is easier to implement the array-based binary heap if the first element is stored at index 1 in the array.

One reason to code up a Priority Queue is that it is a building-block data structure with multiple uses. The Priority Queue conceptually fits well into an abstract data type (ADT) such as a C++/Java/Python class. In fact there are Priority Queue ADTs in all three languages. My recent investigations into functional programming led me to create a Priority Queue using lexical closures. My original class-based Priority Queue was named priq. Thus the functional-closure based version became friq. And indeed it is a friq.
The friq

The screen shot above shows the definition of friq which is function with a single parameter lt. Parameter lt is a comparison "less-than" function which is easier demonstrated than explained. It will be demonstrated in the next section. Note that friq is a function definition that encloses other function definitions, and a rather strange nested list heef. The functionality exported by friq is done with its return statement (see below).

 The functions enqueue and dequeue shown above are the two functions, enclosed by friq, that are exported to the outside world using friq's return statement.
The functions enqueue and dequeue shown above are the two functions, enclosed by friq, that are exported to the outside world using friq's return statement.

 Finally we have the enclosing function friq returning a tuple containing the functions we wish to export.
Finally we have the enclosing function friq returning a tuple containing the functions we wish to export.Demonstrating the friq
The following code demonstrates usage of the friq. A list d is loaded with some random integers. The friq is invoked returning a tuple containing a function to enqueue values and another for dequeueing. List d is iterated and its values are enqueued. Then the friq is drained by dequeueing.

The usage of friq appears reasonably simple and straighforward. Note friq's lt parameter being passed a Python lambda function. The results are seen below.

Next we have a slightly more complex demonstration in which a tuple containing a number and a string is enqueued. Note that the code that handles dequeueing has to do extra work to expand the tuple. Also note that the lambda function is slightly more complex in order to handle the tuple. The index 0 signifies that the sort will be on the tuple's number.

The next demonstration is identifical to the previous with the exception that the lamda function uses an index of 1 which signifies that the sort will be on the tuple's string.

And finally, a display of the results of both demonstrations that involve the (number, str) tuple.

Here is the complete listing of friq.py
friq.py
#! /usr/local/bin/python
def friq(lt):
"""
function friq that returns lexical closure function objects.
param lt - a 'less than' function or lambda
"""
heef = [[None]]
def enqueue(x):
"""
enqueue - visible function
Add to the priority queue
"""
heap = heef[0]
heap.append(x)
up_heap(heap)
def dequeue():
"""
dequeue - visible function
Get the highest priority elemement
"""
value = None
heap = heef[0]
if lenf() > 0:
# The dequeue value is taken from the 2nd element in the array.
# The first element is not used to ease index arithmetic.
value = heap[1]
if lenf() > 1:
# The last element value is copied to the first position.
heap[1] = heap[-1]
# The last value is deleted to reduce the size of the pq by one.
del heap[-1]
if lenf() > 1:
# The val at heap[1] is moved down heap to maintain order.
down_heap(heap)
return value
def heap():
"""
heap - non-visible function
Returns the underlying array-based binary heap.
Can be made visible for debug.
"""
return heef[0]
def lenf():
"""
lenf - non-visible function
Returns the size of the underlying array-based binary heap.
Can be made visible for debug.
"""
return len(heef[0]) - 1
def down_heap(heap):
"""
down-heap - non-visible function
The first element is moved down heap as required
to satisfy heap order.
"""
# px is an index to a bi heap parent
# cx is an index to a bi heap child
px = 1
v = heap[px]
while px <= (len(heap)-1)//2:
# calc the index of the child
cx = px + px
# find the index of the min of the two children
# (if there are two).
if cx < len(heap) - 1 and \
lt(heap[cx + 1], heap[cx]):
cx = cx + 1
# make the comparison - if v is higher pri - we are done.
if lt(v, heap[cx]):
break;
else:
# move the childs value to the parent
heap[px] = heap[cx]
# make the parent index that of the child.
px = cx
# finally the v is set to the current parent
heap[px] = v
def up_heap(heap):
"""
up-heap - non-visible function
The last element is moved up heap to satisfy the heap order.
"""
# cx//2 idenifies cx's parent in the bi heap.
cx = len(heap) - 1
v = heap[cx]
while cx//2 > 0 and lt(v, heap[cx//2]):
heap[cx] = heap[cx//2]
cx = cx//2
heap[cx] = v
# the enclosing function returning functions that are to be visible
return (enqueue, dequeue)